题目内容
3．
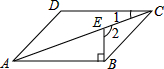如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为110°．
分析 首先由在?ABCD中，∠1=20°，求得∠BAE的度数，然后由BE⊥AB，利用三角形外角的性质，求得∠2的度数．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠BAE=∠1=20°，
∵BE⊥AB，
∴∠ABE=90°，
∴∠2=∠BAE+∠ABE=110°．
故答案为：110°．
点评 此题考查了平行四边形的性质以及三角形外角的性质．注意平行四边形的对边互相平行．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
14．下列运算正确的是（ ）
| A． | 3a+2b=5ab | B． | 3a•2b=6ab | C． | （a3）2=a5 | D． | （ab2）3=ab6 |
11．抛物线y=$\frac{1}{2}{x}^{2}$，y=x2，y=-x2的共同性质是：
①都是开口向上；
②都以点（0，0）为顶点；
③都以y轴为对称轴；
④都关于x轴对称．
其中正确的个数有（ ）
①都是开口向上；
②都以点（0，0）为顶点；
③都以y轴为对称轴；
④都关于x轴对称．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．
五个大小相同的正方体搭成的几何体如图所示，其主视图是（ ）
五个大小相同的正方体搭成的几何体如图所示，其主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC、BE．若AE=6，OA=5，则线段DC的长为4．
在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线交AB于点E，交BC于点D，连接AD，CD=3cm，则BD的长为6cm．
17．分式方程$\frac{2x+1}{3-x}$=1的解是（ ）
| A． | x=-$\frac{1}{2}$ | B． | x=2 | C． | x=3 | D． | x=$\frac{2}{3}$ |