题目内容
11.某校运动会需购买A、B两种奖品.若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.(1)求A、B两种奖品单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,则最多购买B种奖品多少件.
分析 (1)分别利用购买A种奖品3件和B种奖品2件,共需60元;购买A种奖品5件和B种奖品3件,共需95元,得出等式求出答案;
(2)利用购买A、B两种奖品共100件,购买费用不超过1150元,得出不等关系求出答案.
解答 解:(1)设A,B两奖品单价分别为x元和y元,根据题意得
$\left\{\begin{array}{l}{3x+2y=60}\\{5x+3y=95}\end{array}\right.$,
解这个方程组得:
$\left\{\begin{array}{l}{x=10}\\{y=15}\end{array}\right.$,
答:A,B两奖品单价分别为10元和15元;
(2)设购买B种奖品为x件,则A种奖品为(100-x)件,依题意得
10(100-x)+15x≤1150,
解得:x≤30,
答:最多购买B种奖品30件.
点评 此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,根据题意得出正确等量关系是解题关键.

练习册系列答案
相关题目
17.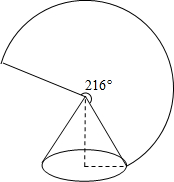 如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
 如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )
如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为( )| A. | 3 | B. | 6 | C. | 3π | D. | 6π |
6.下列根据等式的性质变形正确的是( )
| A. | 由3x-2=2x+2,得x=4 | B. | 由-$\frac{1}{3}x=\frac{2}{3}$,得x=2 | ||
| C. | 由2x-3=3x,得x=3 | D. | 由3x-5=7,得3x=7-5 |

 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为4.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为4. 在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线交AB于点E,交BC于点D,连接AD,CD=3cm,则BD的长为6cm.
在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线交AB于点E,交BC于点D,连接AD,CD=3cm,则BD的长为6cm. 如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED. 如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.
如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.