题目内容
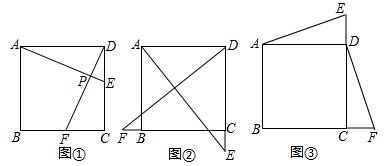
11.如图,在正方形ABCD中,E、F是直线DC、CB上的点,且DE=CF,(1)如图1,当E、F分别在DC、CB边上时,连接AE和DF交于点P,请你写出AE与DF的关系(位置关系和数量关系),并说明理由.
(2)如图2,当E、F分别在DC、CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请直接回答“是”或“否”,不需证明)
(3)如图3,当E、F分别在CD、BC的延长线上时,连接AE和DF,(1)中的结论还成立吗?请说明理由.
分析 (1)先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)由正方形的性质得出AD=DC,∠ADE=∠DCF=90°,DE=CF,SAS证出△ADE≌△DCF,得出AE=DF,∠DAE=∠CDF,证出∠DAE+∠ADF=90°,得出AE⊥DF;
(3)由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF.
解答 解:(1)AE=DF,AE⊥DF;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°,
在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}&{\;}\\{∠ADC=∠C}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴∠APD=90°,
∴AE⊥DF;
故答案为:AE=DF,AE⊥DF;
(2)是;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠DCF=90°,
在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}&{\;}\\{∠ADC=∠C}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴AE⊥DF;
(3)成立;理由如下: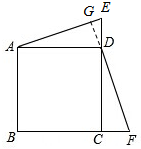 同(1)得:AE=DF,∠DAE=∠CDF,
同(1)得:AE=DF,∠DAE=∠CDF,
延长FD交AE于点G,如图所示:
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,
∴∠AGD=90°,
∴AE⊥DF.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、互余两角的关系、垂线的证法等知识;本题难度较大,综合性强,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案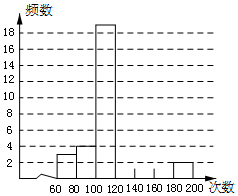 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:176 118 94 144 102 92 113 105 108 60
115 104 126 158 105 132 114 118 152 104
151 165 102 132 112 114 118 114 168 172
105 118 68 126 128 139 84 136 76 145
134 128 126 110 96 148 146 156 186 182
(1)以20为组距,补充并完成频数分布表;
(2)请补充未完成的频数直方分布图;
| 次数分组 | 频数 |
| 60≤x<80 | 3 |
| 80≤x<100 | 4 |
| 100≤x<120 | 19 |
| 120≤x<140 | 10 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 2 |
| 合计 | 50 |
| 摸球的次数n | 200 | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数m | 117 | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率 $\frac{n}{m}$ | 0.585 | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
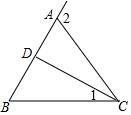 已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )
已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )| A. | ∠2>∠B+∠1 | B. | ∠2=∠B+∠1 | C. | ∠2<∠B+∠1 | D. | 无法确定 |
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁品 | |
| D. | 调查某市初中生的睡眠情况 |
| A. | -2 | B. | $\frac{3}{2}$ | C. | 0.5 | D. | 1 |
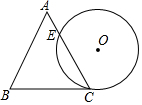 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
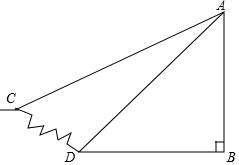 如图,某同学自某观景平台AB上的A处看到有一个11阶的楼梯,他测得最上面楼梯角C的俯角为40°,最下面楼梯角D的俯角为45°,若每个台阶的高为15cm,宽为30cm,试求观景平台的高AB(同学身高忽略不计).(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{2}≈1.41$)
如图,某同学自某观景平台AB上的A处看到有一个11阶的楼梯,他测得最上面楼梯角C的俯角为40°,最下面楼梯角D的俯角为45°,若每个台阶的高为15cm,宽为30cm,试求观景平台的高AB(同学身高忽略不计).(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{2}≈1.41$)