题目内容
1.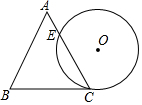 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
分析 连接OC,并过点O作OF⊥CE于F,求出等边三角形的高即可得出圆的直径,继而得出OC的长度,根据切线的性质和等边三角形的性质求得∠OCF=30°,进一步求得∠COE=120°,根据弧长公式即可求得.
解答  解:连接OC,OE,并过点O作OF⊥CE于F,
解:连接OC,OE,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4cm,
∴△ABC的高为2$\sqrt{3}$cm,
∴OC=$\sqrt{3}$cm,
∵⊙O与BC相切于点C,
∴∠OCB=90°,
又∵∠ACB=60°,
∴∠OCF=30°,
∵OE=OC,
∴∠OEF=∠OCF=30°,
∴∠COE=120°,
∴弧CE的长=$\frac{120π×\sqrt{3}}{180}$=$\frac{2\sqrt{3}π}{3}$,
故选C.
点评 本题主要考查了切线的性质,等边三角形的性质和弧长公式的有关知识,题目不是太难,属于基础性题目.

练习册系列答案
相关题目
9.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解商丘市的空气质量情况 | B. | 了解包河的水污染情况 | ||
| C. | 了解商丘市居民的环保意识 | D. | 了解全班同学每周体育锻炼的时间 |
6.下列运算正确的是( )
| A. | x3+x2=x5 | B. | x3•x2=x6 | C. | (x3)2=x9 | D. | x3÷x2=x |
11.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.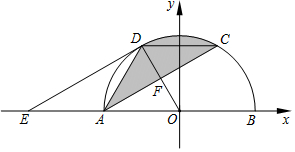 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作DE∥AC,交BA的延长线于点E,连接AD,CD.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作DE∥AC,交BA的延长线于点E,连接AD,CD.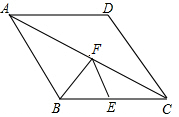 如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )
如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )