题目内容
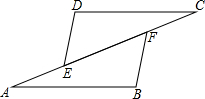如图，AB∥CD，AE=CF，AB=CD．求证：DE=BF．考点：全等三角形的判定与性质
专题：
分析：利用三角形全等的判定定理证得△ABF≌△CDE，进一步得出DE=BF即可．
解答：证明：∵AB∥CD，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
即AF=CE，
在△ABF和△CDE中，
∴△ABF≌△CDE，
∴DE=BF．
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
即AF=CE，
在△ABF和△CDE中，
|
∴△ABF≌△CDE，
∴DE=BF．
点评：本题考查了全等三角形的判定与性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
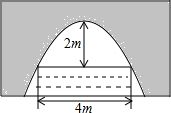有一座抛物线形拱桥，正常水位时桥下水面宽度为4m，拱顶距离水面 2m．
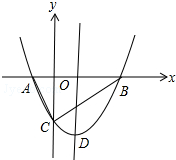如图，抛物线y=x2+bx-2与x轴交于A，B两点，与y轴交于C点，且A（-1，0）．
如图所示，已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2cm的速度向左运动，最终点A与点M重合．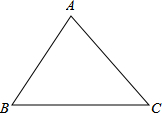
从三角形木板上截下一块圆形的木板，