题目内容
 如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合.
如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合.(1)求重叠部分面积(即图中阴影面积)y(cm2)与时间t(s)之间的函数关系式.
(2)经过几秒钟重叠部分面积等于8cm2?
考点:一元二次方程的应用,根据实际问题列二次函数关系式
专题:几何动点问题
分析:(1)根据△ABC是等腰直角三角形,则重叠部分也是等腰直角三角形,根据三角形的面积公式即可求解;
(2)根据等量关系:重叠部分面积等于8cm2,列出方程求解即可.
(2)根据等量关系:重叠部分面积等于8cm2,列出方程求解即可.
解答:解:(1)AM=20-2t,
则重叠部分面积y=
(20-2t)2;
(2)当y=8时,
(20-2t)2=8,
解得t1=8,t2=12(舍去)
故经过8秒钟重叠部分面积等于8cm2.
则重叠部分面积y=
| 1 |
| 2 |
(2)当y=8时,
| 1 |
| 2 |
解得t1=8,t2=12(舍去)
故经过8秒钟重叠部分面积等于8cm2.
点评:考查了一元二次方程的应用.根据题意,找到所求量的等量关系是解决问题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
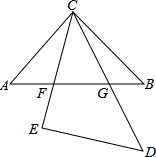 如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.
如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.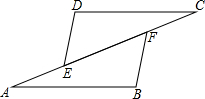 如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.
如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.