题目内容
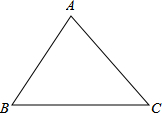 从三角形木板上截下一块圆形的木板,
从三角形木板上截下一块圆形的木板,(1)怎样才能使圆的面积尽可能大?(不写作法,但要保留作图痕迹)
(2)若△ABC的三边长为AB=4,BC=5,AC=6,求△ABC的面积;
(3)在(1)、(2)的基础上,求最大圆铁皮的半径.
考点:三角形的内切圆与内心,作图—复杂作图
专题:
分析:(1)利用尺规作图法直接作△ABC的内切圆;
(2)作BC边上的高AM,运用勾股定理求出AM的长即可解决问题.
(3)连接OA、OB、OC、OD、OE、OF;运用△ABC的面积=△OAB、△OBC、△OAC的面积之和,即可解决问题.
(2)作BC边上的高AM,运用勾股定理求出AM的长即可解决问题.
(3)连接OA、OB、OC、OD、OE、OF;运用△ABC的面积=△OAB、△OBC、△OAC的面积之和,即可解决问题.
解答:解:(1)如图1所示,作△ABC的内切圆O;

(2)过点A作AM⊥BC于点M,设BM=x,则CM=5-x;
由勾股定理得:AB2-BM2=AM2,AC2-CM2=AM2,
故42-x2=62-(5-x)2,整理得10x=5,
∴x=
,AM=
=
,
∴S△ABC=
BC•AM=
×5×
=
.
(3)设⊙O的半径为r,
∵S△ABC=S△OAB+S△OBC+S△OAC
=
+
+
=
,
∴
=
,
解得r=
,
∴最大圆铁皮的半径为
.

(2)过点A作AM⊥BC于点M,设BM=x,则CM=5-x;
由勾股定理得:AB2-BM2=AM2,AC2-CM2=AM2,
故42-x2=62-(5-x)2,整理得10x=5,
∴x=
| 1 |
| 2 |
42-(
|
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
5
| ||
| 4 |
(3)设⊙O的半径为r,
∵S△ABC=S△OAB+S△OBC+S△OAC
=
| AB•OD |
| 2 |
| BC•OE |
| 2 |
| AC•OF |
| 2 |
| 15r |
| 2 |
∴
5
| ||
| 4 |
| 15r |
| 2 |
解得r=
| ||
| 6 |
∴最大圆铁皮的半径为
| ||
| 6 |
点评:本题以三角形为载体在考查三角形内切圆的作法的同时,还渗透了对勾股定理等几何知识的考查,对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
下列运算正确的是( )
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、2a-2=
|
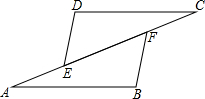 如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF.
如图,AB∥CD,AE=CF,AB=CD.求证:DE=BF. 在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当
在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当 如图是由六个棱长为1的小正方体组成的几何体,其俯视图的面积是
如图是由六个棱长为1的小正方体组成的几何体,其俯视图的面积是