题目内容
7. 已知:如图,?ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF.
已知:如图,?ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF.(1)求证:△FBE≌△COE;
(2)将?ABCD添加一个条件,使四边形AFBO是菱形,并说明理由.
分析 (1)由AAS证得两个三角形全等即可.
(2)当平行四边形ABCD的对角线相等,即平行四边形ABCD是矩形时,四边形AFBO是菱形.
解答 (1)证明:如图,取BC的中点G,连接EG.
∵E是BO的中点,
∴EG是△BFC的中位线,
∴EG=$\frac{1}{2}$BF.
同理,EG=$\frac{1}{2}$OC,
∴BF=OC.
又∵四边形ABCD是平行四边形,
∴AO=CO,
∴BF=OC.
又∵BF∥AC,
∴∠FBE=∠COE.
在△FBE△COE中,$\left\{\begin{array}{l}{∠OEC=∠BEF}&{\;}\\{∠EOC=∠EBF}&{\;}\\{OC=BF}&{\;}\end{array}\right.$,
∴△FBE≌△COE(AAS);
(2)解:当AC=BD时,四边形AFBO是菱形.理由如下:
∵AC=BD,
∴平行四边形ABCD是矩形,
∴OA=OC=OB=OD,
∴平行四边形AFBO是菱形.
点评 本题考查了平行四边形的判定与性质以及菱形的判定,有利于学生思维能力的训练.涉及的知识点有:有一组邻边相等的平行四边形是菱形;矩形的对角线相等.

练习册系列答案
相关题目
18. 将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.
将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.
 将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.
将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.| A. | 100 | B. | 121 | C. | 144 | D. | 169 |
 (1)解方程:x(x-2)+x-2=0
(1)解方程:x(x-2)+x-2=0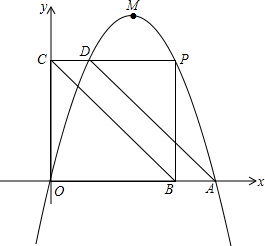 在平面直角坐标系xOy中,抛物线y=-x2+4x与x轴的正半轴交于点A,其顶点为M,点P是该抛物线上位于A、M两点之间的部分上的动点,过点P作PB⊥x轴于点B,PC⊥y轴于点C,且交抛物线于点D,连接BC,AD,OP,当四边形ABCD被OP分成的两部分面积比为1:2时,点P的坐标为($\frac{12}{5}$,$\frac{96}{25}$).
在平面直角坐标系xOy中,抛物线y=-x2+4x与x轴的正半轴交于点A,其顶点为M,点P是该抛物线上位于A、M两点之间的部分上的动点,过点P作PB⊥x轴于点B,PC⊥y轴于点C,且交抛物线于点D,连接BC,AD,OP,当四边形ABCD被OP分成的两部分面积比为1:2时,点P的坐标为($\frac{12}{5}$,$\frac{96}{25}$).