题目内容
15．一组数据23、24、25、26、27的标准差是$\sqrt{2}$．分析 首先求出平均数，用方差公式求出方差，再开平方即可．
解答 解：$\overline{x}$=$\frac{1}{5}$×（23+24+25+26+27）=25，
方差S2=$\frac{1}{5}$[（23-25）2+（24-25）2+（25-25）2+（26-25）2+（27-25）2]
=$\frac{1}{5}$[（-2）2+（-1）2+02+12+22]=2
故五个数据的标准差是S=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查的是标准差的计算，计算标准差需要先算出方差，计算方差的步骤是：①计算数据的平均数；②计算偏差，即每个数据与平均数的差；③计算偏差的平方和；④偏差的平方和除以数据个数．标准差即方差的算术平方根；注意标准差和方差一样都是非负数．
练习册系列答案
相关题目
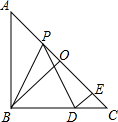如图，在等腰直角△ABC中，O是斜边AC的中点，P是斜边AC上的一个动点，D为BC上的一点，且PB=PD，DE⊥AC，垂足为E．
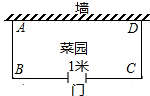如图，用长为39米的篱笆（虚线部分），一面靠墙围成矩形ABCD菜园（AB＜BC，且在边BC上开一个1米宽的门．要使围成的矩形ABCD菜园面积为128米2，那么矩形一边AB长应为多少米？
如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D，以AB上一点O为圆心作⊙O，使⊙O经过点A和点D．
已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于E，交BC边于F，分别连接AF和CE，AE=10．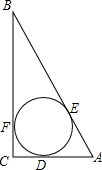
如图，⊙O为Rt△ABC的内切圆，⊙O的半径r=1，∠B=30°，