Question

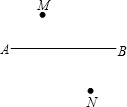如图，一辆汽车在笔直的公路AB上由A向B行驶，M、N分别是位于公路AB两侧的村庄．设汽车行驶到点P时，离村庄M最近，汽车行驶到点Q时，离村庄N最近，汽车行驶到点O时，离村庄M、N的距离和最小，请在图中公路AB上分别画出点P、Q、O的位置，并简要说明数学原理．

Answer 1

考点：作图—应用与设计作图

专题：

分析：要使距离最短，根据垂线段定理，点到直线的距离最短时与直线垂直，所以只要从M、N两点向AB作垂线；根据平面内两点之间线段最短，连接MN即可得出Q点位置．

解答：解：作MP⊥AB，NQ⊥AB，垂足分别是点P，Q，连接MN交AB于O．

点评：此题主要考查了垂线段的性质以及两点之间线段最短问题，正确将实际问题转化为数学知识是解题关键．在这种设计作图题中，任何一个知识点都可能考到，所以要对每个知识点都有很好的了解．