题目内容
 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点,AD=3,BC=5,则AB的长度为
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点,AD=3,BC=5,则AB的长度为考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,然后利用“HL”证明Rt△ADE和Rt△AFE全等,根据全等三角形对应边相等可得AF=AD,再根据线段中点的定义可得DE=EC,从而得到EC=EF,同理可得BF=BC,然后根据AB=AF+BF计算即可得解.
解答: 解:如图,过点E作EF⊥AB于F,
解:如图,过点E作EF⊥AB于F,
∵DC⊥AD,AE平分∠BAD,
∴DE=EF,
在Rt△ADE和Rt△AFE中,
,
∴Rt△ADE≌Rt△AFE(HL),
∴AF=AD=3,
∵E是DC的中点,
∴DE=EC,
∴EC=EF,
同理可得BF=BC=5,
∴AB=AF+BF=3+5=8.
故答案为:8.
 解:如图,过点E作EF⊥AB于F,
解:如图,过点E作EF⊥AB于F,∵DC⊥AD,AE平分∠BAD,
∴DE=EF,
在Rt△ADE和Rt△AFE中,
|
∴Rt△ADE≌Rt△AFE(HL),
∴AF=AD=3,
∵E是DC的中点,
∴DE=EC,
∴EC=EF,
同理可得BF=BC=5,
∴AB=AF+BF=3+5=8.
故答案为:8.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
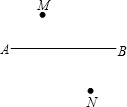 如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,离村庄M、N的距离和最小,请在图中公路AB上分别画出点P、Q、O的位置,并简要说明数学原理.
如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,离村庄M、N的距离和最小,请在图中公路AB上分别画出点P、Q、O的位置,并简要说明数学原理. 如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥AB于点H,且DH与AC交于G,则DH=
如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥AB于点H,且DH与AC交于G,则DH= 如图,∠ABC=70°,∠A=50°,AB的垂直平分线交AC于D,则∠DBC=
如图,∠ABC=70°,∠A=50°,AB的垂直平分线交AC于D,则∠DBC=