题目内容
16.在某超市小明买了1千克甲种糖果和2千克乙种糖果,共付38元;小强买了2千克甲种糖果和0.5千克乙种糖果,共付27元.(1)求该超市甲、乙两种糖果每千克各需多少元?
(2)某顾客到该超市购买甲、乙两种糖果共20千克混合,欲使总价不超过240元,问该顾客混合的糖果中甲种糖果最少多少千克?
分析 (1)设超市甲种糖果每千克需x元,乙种糖果每千克需y元.根据“1千克甲种糖果和2千克乙种糖果,共付38元;小强买了2千克甲种糖果和0.5千克乙种糖果,共付27元”列出方程组并解答;
(2)设购买甲种糖果a千克,则购买乙种糖果(20-a)千克,结合“总价不超过240元”列出不等式,并解答.
解答 解:(1)设超市甲种糖果每千克需x元,乙种糖果每千克需y元,
依题意得:$\left\{\begin{array}{l}{x+2y=38}\\{2x+0.5y=27}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=10}\\{y=14}\end{array}\right.$.
答:超市甲种糖果每千克需10元,乙种糖果每千克需14元;
(2)设购买甲种糖果a千克,则购买乙种糖果(20-a)千克,
依题意得:10a+14(20-a)≤240,
解得a≥10,
即a最小值=10.
答:该顾客混合的糖果中甲种糖果最少10千克.
点评 本题考查了一元一次不等式和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系.

练习册系列答案
相关题目
6. 如图所示,a与b的大小关系是( )
如图所示,a与b的大小关系是( )
 如图所示,a与b的大小关系是( )
如图所示,a与b的大小关系是( )| A. | a<b | B. | a>b | C. | a=b | D. | b=2a |
4.n是整数,式子$\frac{1}{8}$[1-(-1)n](n2-1)计算的结果( )
| A. | 是0 | B. | 总是奇数 | ||
| C. | 总是偶数 | D. | 可能是奇数也可能是偶数 |
11.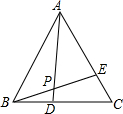 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
1.不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1>0}\\{3-x≥2}\end{array}\right.$的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. | 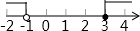 |
8.若某三角形的两边长是3和4,则下列长度的线段能作为其第三边的是( )
| A. | 10 | B. | 9 | C. | 7 | D. | 5 |
5.在下列各实数中,属于无理数的是( )
| A. | 0.23 | B. | -$\frac{22}{7}$ | C. | $\frac{π}{3}$ | D. | $\sqrt{16}$ |
6.下列计算正确的是( )
| A. | ($\sqrt{2}$)2=2 | B. | $\sqrt{3}$-$\sqrt{2}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=3 | D. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ |