题目内容
14. 将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.
将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.
分析 设菱形AECF的边长为x,根据矩形的性质得到∠B=90°,根据勾股定理列出方程,解方程求出x的值,根据菱形的面积公式计算即可.
解答 解:设菱形AECF的边长为x,则BE=8-x,
∵四边形ABCD为矩形,
∴∠B=90°,
由勾股定理得,BE2+AB2=AE2,即(8-x)2+42=x2,
解得,x=5,即EC=5,
∴菱形AECF的面积=EC•AB=20.
点评 本题考查的是菱形的性质、矩形的性质、翻折变换的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.n是整数,式子$\frac{1}{8}$[1-(-1)n](n2-1)计算的结果( )
| A. | 是0 | B. | 总是奇数 | ||
| C. | 总是偶数 | D. | 可能是奇数也可能是偶数 |
5.在下列各实数中,属于无理数的是( )
| A. | 0.23 | B. | -$\frac{22}{7}$ | C. | $\frac{π}{3}$ | D. | $\sqrt{16}$ |
9.下列各式中①$\sqrt{\frac{1}{2}}$,②$\sqrt{2x}$,③$\sqrt{{x}^{3}}$,④$\sqrt{-5}$,⑤$\root{3}{5}$,二次根式的个数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列计算正确的是( )
| A. | ($\sqrt{2}$)2=2 | B. | $\sqrt{3}$-$\sqrt{2}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=3 | D. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ |
4.已知直线y=-x+m经过了(1,0)点,则关于x的不等式-x+m≥0的解集为( )
| A. | x<1 | B. | x>1 | C. | x≤1 | D. | 不确定 |
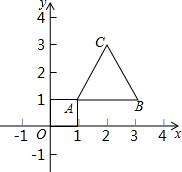 如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1).
如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1).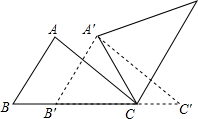 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.