题目内容
16.如图,在平面直角坐标系中,点A,B的坐标分别为(-5,0),(3,0).现同时将点A,B向上平移4个单位,再向右平移3个单位,得到点A,B的对应点分别是D,C.连按AD,BC,CD.(I)点C的坐标(6,4),点D的坐标(-2,4).
(2)动点P从D点出发,以每秒2个单位长的连度沿折线D→C→B向终点B匀速运动.同时另一动点Q从B点出发,以每砂1个单位长的速度沿折线B→C→D向终点D匀速运动,当一点到达终点时,另一点停止运动,设运动时间为t秒,BC线段长为5,求t为何值时,PC=QC.
(3)点E是线段AB的中点,过点E作EF垂直于x轴.点Q为直线EF上的一个动点,连接AC,AQ,CQ,当三角形ACQ的面积为25时,求点Q的坐标.

分析 (1)根据平移规律即可解决问题.
(2)分两种情形讨论)①当点P在线段CD上时,由题意8-2t=5-t,②当P与Q相遇时,由题意2t+t=13,解方程即可.
(3)如图,连接AC交EF于H,设Q(-1,m),直线AC的解析式为y=kx+b,求出直线AC的解析式,可得H(-1,$\frac{16}{11}$),根据三角形的面积公式,列出方程计算即可.
解答 解:(1)由题意可知C(6,4),D(-2,4).
故答案为C(6,4),D(-2,4).
(2)①当点P在线段CD上时,由题意8-2t=5-t,解得t=3.
②当P与Q相遇时,由题意2t+t=13,解得t=$\frac{13}{3}$.
综上所述,t=s或$\frac{13}{3}$s时,PC=QC.
(3)如图,连接AC交EF于H,设Q(-1,m),直线AC的解析式为y=kx+b,
∵A(-5,0),C(6,4),则有$\left\{\begin{array}{l}{-5k+b=0}\\{6k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{11}}\\{b=\frac{20}{11}}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{4}{11}$x+$\frac{20}{11}$,
∴H(-1,$\frac{16}{11}$),
∵三角形ACQ的面积为25,
∴$\frac{1}{2}$•|m-$\frac{16}{11}$|•11=25,
∴m=-$\frac{34}{11}$或6,
∴满足条件的点Q坐标为(-1,6)或(-1,-$\frac{34}{11}$).
点评 本题考查几何变换综合题、一元一次方程的应用、一次函数的应用、三角形的面积等知识,解题的关键是学会构建方程解决实际问题,属于中考常考题型.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案| 方式一 | 方式二 | |
| 月租费 | 30元/月 | 0元 |
| 本地的通话费 | 0.30元/分 | 0.40元/分 |
(2)对于某个本地通话时间,通话时间多少分钟时会出现按两种计费方式收费一样多?(此问列方程解)
 如图,下列条件中,能判定AB∥CD的是( )
如图,下列条件中,能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠4=∠6 | C. | ∠4=∠5 | D. | ∠1+∠3=180° |
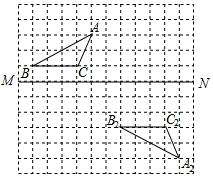 在边长为1的正方形网格中,
在边长为1的正方形网格中,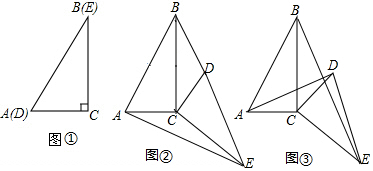
 如图所示是某个正方体的平面展开图,其中每个面上都标有一个数字,那么在原正方体中,相对的面上的两个数字的乘积是负数的有2对.
如图所示是某个正方体的平面展开图,其中每个面上都标有一个数字,那么在原正方体中,相对的面上的两个数字的乘积是负数的有2对.