题目内容
13.满足下列条件的△ABC,不是直角三角形的是( )| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A=∠B-∠C | ||
| C. | AB2=AC2-BC2 | D. | AB=5,BC=12,AC=13 |
分析 分别根据勾股定理、三角形内角和定理对各选项进行逐一判断即可.
解答 解:A、当∠A:∠B:∠C=3:4:5时,可设∠A=3x°,∠B=4x°,∠C=5x°,由三角形内角和定理可得3x+4x+5x=180,解得x=15°,所以∠A=45°,∠B=60°,∠C=75°,所以△ABC为锐角三角形,故本选项正确;
B、∵∠A=∠B-∠C,∴∠A+∠C=∠B,∵∠A+∠B+∠C=180°,∴2∠B=180°,解得∠B=90°,
故本选项错误;
C、∵AB2=AC2-BC2,∴AB2+BC2=AC2,∴△ABC是直角三角形,故本选项错误;
D、∵52+122=132,即AB2+BC2=AC2,∴△ABC是直角三角形,故本选项错误.
故选A.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知a,b互为相反数,且满足ax-b=0(a≠0),则x等于( )
| A. | 1 | B. | -1 | C. | -1或1 | D. | 任意有理数 |
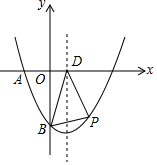 如图,在平面直角坐标系中,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A(-2,0)、C两点,与y轴交于点B(0,-4),其对称轴与x轴交于点D.
如图,在平面直角坐标系中,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A(-2,0)、C两点,与y轴交于点B(0,-4),其对称轴与x轴交于点D.