题目内容
18.已知直线y=kx+b过点P(-2,1),且与x轴的负半轴交于点A,与y轴的正半轴交于点B,当△AOB面积最小时,求k、b的值.分析 根据函数图象上点的坐标特征得到k与b的关系,用k表示出点A、点B的坐标,根据三角形的面积公式解答即可.
解答 解:∵直线y=kx+b过点P(-2,1),
∴-2k+b=1,即b=2k+1,
则直线的解析式为y=kx+2k+1,
当x=0时,y=2k+1,
当y=0时,x=$\frac{-2k-1}{k}$,
则点A的坐标为:($\frac{-2k-1}{k}$,0),点B的坐标为:(0,2k+1),
△AOB面积=$\frac{1}{2}$×|$\frac{-2k-1}{k}$|×|2k+1|=$\frac{1}{2}$×|k+$\frac{1}{k}$+4|,
由题意得,k>0,
则k+$\frac{1}{k}$≥2,
当△AOB面积取最小值时,k=1,
则b=3,
答:k=1,b=3.
点评 本题考查的是一次函数图象上点的坐标特征,根据题意确定点A、点B的坐标是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
13.满足下列条件的△ABC,不是直角三角形的是( )
| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A=∠B-∠C | ||
| C. | AB2=AC2-BC2 | D. | AB=5,BC=12,AC=13 |
14.cos60°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
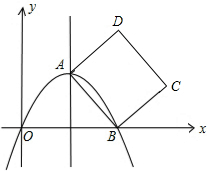 如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )
如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )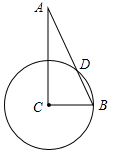 如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.
如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.