题目内容
8.P为线段AB的黄金分割点,AP>BP,如果AP=10cm,那么BP=6.2cm.(精确到0.1cm)分析 设BP=x,根据黄金比的定义列出算式,求解即可;把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.
解答 解:设BP=x,根据题意得:
($\frac{\sqrt{5}-1}{2}$)×(10+x)=10,
解得:x=5$\sqrt{5}$-5,
则BP=(5$\sqrt{5}$-5)≈6.2cm.
故答案为:6.2.
点评 本题考查了黄金分割:记住黄金分割的定义是解决此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
13.满足下列条件的△ABC,不是直角三角形的是( )
| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A=∠B-∠C | ||
| C. | AB2=AC2-BC2 | D. | AB=5,BC=12,AC=13 |
20.用公式法解方程x2-4x-2=0,其中b2-4ac的值是( )
| A. | 16 | B. | 24 | C. | 8 | D. | 4 |
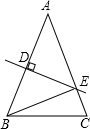 如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.