题目内容
4.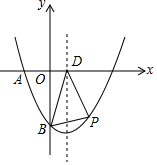 如图,在平面直角坐标系中,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A(-2,0)、C两点,与y轴交于点B(0,-4),其对称轴与x轴交于点D.
如图,在平面直角坐标系中,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A(-2,0)、C两点,与y轴交于点B(0,-4),其对称轴与x轴交于点D.(1)求该二次函数的解析式及点C的坐标;
(2)若点P是第四象限内该二次函数图象上的一个动点,连接PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
分析 (1)把点A(-2,0)和点B(0,-4)坐标代入二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)求出a、c的值,得到二次函数的解析式,解方程求出点C的坐标;
(2)设点P的坐标为(x,$\frac{1}{4}$x2-$\frac{3}{2}$x-4),根据梯形的面积公式和三角形的面积公式计算求出△BDP面积,根据二次函数的性质解答.
解答 解:(1)∵二次函数y=ax2-$\frac{3}{2}$x+c的图象与x轴交于A(-2,0),与y轴交于点B(0,-4),
∴$\left\{\begin{array}{l}{4a+3+c=0}\\{c=-4}\end{array}\right.$,
解得,a=$\frac{1}{4}$,c=-4,
则二次函数的解析式为y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4,
$\frac{1}{4}$x2-$\frac{3}{2}$x-4=0,
x1=-2,x2=8,
∴点C的坐标为(8,0);
(2)设点P的坐标为(x,$\frac{1}{4}$x2-$\frac{3}{2}$x-4),
y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{4}$(x-3)2-$\frac{25}{4}$,
△BDP面积=$\frac{1}{2}$×(4-$\frac{1}{4}$x2+$\frac{3}{2}$x+4)×x-$\frac{1}{2}$×3×4-$\frac{1}{2}$×(x-3)×(-$\frac{1}{4}$x2+$\frac{3}{2}$x+4)=-$\frac{3}{4}$x2+$\frac{17}{2}$x=-$\frac{3}{4}$(x-$\frac{17}{3}$)2+$\frac{289}{12}$,
∴当x=$\frac{17}{3}$时,△BDP面积的最大,此时点P的坐标为($\frac{17}{3}$,$\frac{161}{36}$).
点评 本题考查的是抛物线与x轴的交点、二次函数的最值以及待定系数法求函数解析式,掌握二次函数的性质、灵活运用待定系数法是解题的关键.

| A. | (-3)-1 | B. | (-3)0 | C. | (-3)-2 | D. | (-3x)-3 |
| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A=∠B-∠C | ||
| C. | AB2=AC2-BC2 | D. | AB=5,BC=12,AC=13 |
| A. | 16 | B. | 24 | C. | 8 | D. | 4 |
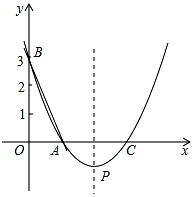 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.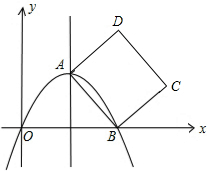 如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )
如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )