题目内容
1.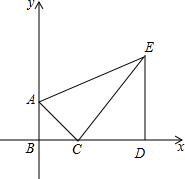 已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.
已知,如图,B为坐标原点,A(0,3),D(10,0),E(10,8),点C是线段BD上的动点.(1)求线段AB,ED的长.
(2)求满足△ABC与△CDE相似时的C点坐标.
(3)当△ABC与△CDE相似时,求△ABC与△CDE的面积之比.
分析 (1)根据已知条件即可得到结论;
(2)分两种情况讨论:若△ABC与△CDE相似,设BC=x,则CD=10-x,①当AB与CD是对应边,根据相似三角形的性质得到比例式$\frac{AB}{CD}=\frac{BC}{DE}$,即$\frac{3}{10-x}=\frac{x}{8}$,解得:x=4,或x=6,即可求出结果,②当AB与ED是对应边,根据相似三角形的性质得到比例式$\frac{AB}{ED}=\frac{BC}{CD}$,即$\frac{3}{8}=\frac{x}{10-x}$,解得:x=$\frac{30}{11}$,即可得到结果;
(3)分三种情况:①当C(4,0)时,CD=6,当C(6,0)时,CD=4,③当AB与ED是对应边,根据相似三角形的性质即可得到结论.
解答 解:(1)∵ B为坐标原点,A(0,3),D(10,0),E(10,8),
B为坐标原点,A(0,3),D(10,0),E(10,8),
∴AB=3,ED=8;
(2)若△ABC与△CDE相似,设BC=x,则CD=10-x,
①当AB与CD是对应边,
∴$\frac{AB}{CD}=\frac{BC}{DE}$,即$\frac{3}{10-x}=\frac{x}{8}$,
解得:x=4,或x=6,
∴C(4,0),或(6,0);
②当AB与ED是对应边,
∴$\frac{AB}{ED}=\frac{BC}{CD}$,即$\frac{3}{8}=\frac{x}{10-x}$,
解得:x=$\frac{30}{11}$,
∴C($\frac{30}{11}$,0);
综上所述:点C的坐标为:(4,0),(6,0),($\frac{30}{11}$,0);
(3)①当C(4,0)时,CD=6,
∴$\frac{{S}_{△ABC}}{{S}_{△CDE}}$=($\frac{AB}{CD}$)2=$\frac{1}{4}$,
②当C(6,0)时,CD=4,
∴$\frac{{S}_{△ABC}}{{S}_{△CDE}}$=($\frac{AB}{CD}$)2=$\frac{9}{16}$,
③当AB与ED是对应边,
∴$\frac{{S}_{△ABC}}{{S}_{△CDE}}$=($\frac{AB}{DE}$)2=$\frac{9}{64}$,
综上所述:当△ABC与△CDE相似时,△ABC与△CDE的面积之比为:$\frac{1}{4}$,$\frac{9}{16}$,$\frac{9}{64}$.
点评 本题考查了相似三角形的判定和性质,动点问题,找准对应边是解题的关键.

| A. | m$>\frac{7}{4}$ | B. | m$≥\frac{7}{4}$ | C. | m$<\frac{7}{4}$ | D. | m$≤\frac{7}{4}$ |
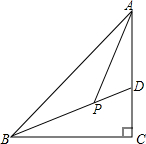 如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.
如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.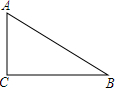 如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r.
如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r.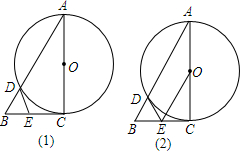
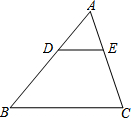 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=6,则BC的长为15.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=6,则BC的长为15.
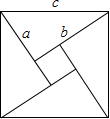 勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.
勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.