题目内容
13.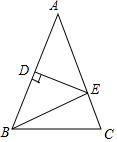 如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.
如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.(1)若∠A=50°,求∠EBC的度数.
(2)若AB=8,△BEC的周长是11,求△ABC的周长.
分析 (1)由等腰三角形的性质可求得∠ABC,由线段垂直平分线的性质可求得∠ABE,则可求得∠EBC;
(2)由线段垂直平分线的性质可求得BE+EC+BC=AE+EC+BC=AC+BC,再结合△BEC的周长,可求得BC的长,进一步得到△ABC的周长.
解答 解:(1)∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°.
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=50°.
∴∠DBC=15°.
(2)∵AE=BE,AB=8,
∴BE+CE=8.
∵△BEC的周长是11,
∴BC=3,
∴△ABC的周长是8+8+3=19.
点评 本题主要考查等腰三角形的性质,线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 三角形的内心到三角形的三个顶点的距离相等 | |
| B. | 三点确定一个圆 | |
| C. | 垂直于半径的直线一定是这个圆的切线 | |
| D. | 任何三角形有且只有一个内切圆 |
2.△ABC是不规则三角形,若线段AD把△ABC分为面积相等的两部分,则线段AD应该是( )
| A. | 三角形的角平分线 | B. | 三角形的中线 | ||
| C. | 三角形的高 | D. | 以上都不对 |
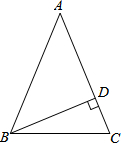 如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.
如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.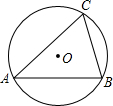 如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.
如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.