题目内容
1．求下列各式中的x．（1）x2=81；
（2）16x2-25=0．
分析 （1）两边开方，即可得出两个一元一次方程，求出方程的解即可；
（2）先分解因式，即可得出两个一元一次方程，求出方程的解即可．
解答 解：（1）两边开方得：x=±9，
即x1=9，x2=-9；
（2）分解因式得：（4x+5）（4x-5）=0，
4x+5=0，4x-5=0，
x1=-$\frac{5}{4}$，x2=$\frac{5}{4}$．
点评 本题考查了解一元二次方程的应用，能把一元二次方程转化成一元一次方程是解此题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知△ABC中，AC=6cm，BC=8cm，AB=10cm，CD为AB边上的高．动点P从点A出发，沿着△ABC的三条边逆时针走一圈回到A点，速度为2cm/s，设运动时间为ts．
12．下列说法错误的是（ ）
| A． | 2x2-3xy-1是二次三项式 | B． | -x+1是多项式 | ||
| C． | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D． | x与π是同类项 |
9．如图，在数轴上放置一个长方形块，长方形的长为$\frac{3}{4}$，宽为$\frac{1}{3}$．此时将长方形沿数轴正方向做顺时针的翻动．长方形所在的初始位置如图中实线所示，沿A点（如图所示）做数轴的垂线，在数轴上所对应的数字是1．
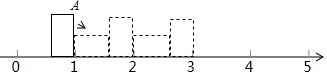
（1）第3次翻动长方形块后，A点在数轴上所对应的数字表示是$\frac{25}{12}$
（2）第8次翻动长方形块后，A点在数轴上所对应的数字表示是5$\frac{1}{3}$
（3）第101次翻动长方形块后，A点在数轴上所对应的数字表示是55$\frac{11}{12}$．
| 翻动次数 | A点在数轴上对应的数字 |
| 1 | 1+$\frac{3}{4}$ |
| 2 | 1+$\frac{3}{4}$+0 |
| 3 | |
| 4 |
（2）第8次翻动长方形块后，A点在数轴上所对应的数字表示是5$\frac{1}{3}$
（3）第101次翻动长方形块后，A点在数轴上所对应的数字表示是55$\frac{11}{12}$．
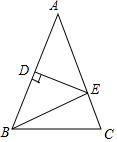如图，△ABC中，AB=AC，DE垂直平分AB，D为垂足交AC于E．