题目内容
2.△ABC是不规则三角形,若线段AD把△ABC分为面积相等的两部分,则线段AD应该是( )| A. | 三角形的角平分线 | B. | 三角形的中线 | ||
| C. | 三角形的高 | D. | 以上都不对 |
分析 作三角形ABC的高AE,根据三角形面积公式,分别表示出S△ABD和S△ACD,即可得出BD=CD,即线段AD是三角形的中线.
解答 解:作AE⊥BC,
∴S△ABD=$\frac{1}{2}$×BD×AE,
S△ACD=$\frac{1}{2}$×CD×AE,
∵S△ABD=S△ACD,
即$\frac{1}{2}$×BD×AE=$\frac{1}{2}$×CD×AE,
∴BD=CD,
即线段AD是三角形的中线.
故选B
点评 本题主要考查了三角形的面积和三角形的中线,三角形的中线可分三角形为面积相等的两部分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法错误的是( )
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1是多项式 | ||
| C. | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D. | x与π是同类项 |
17.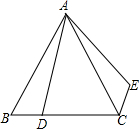 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )| A. | 75° | B. | 60° | C. | 45° | D. | 15° |
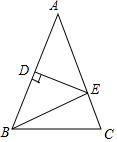 如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.
如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.