题目内容
12．
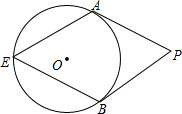如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠E=64°，则∠P=52度．
分析 连接OA，BO，由圆周角定理知可知∠AOB=2∠E=128°，PA、PB分别切⊙O于点A、B，利用切线的性质可知∠OAP=∠OBP=90°，根据四边形内角和可求得∠P=180°-∠AOB=52°．
解答 
解：连接OA，BO；
∵∠AOB=2∠E=128°，
∴∠OAP=∠OBP=90°，
∴∠P=180°-∠AOB=52°．
故答案为：52．
点评 本题主要考查了切线的性质和切线长定理，综合运用圆周角定理，切线的性质，四边形的内角和为360度求解．
练习册系列答案
阅读快车系列答案
相关题目
3．
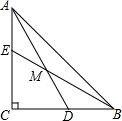如图，△ABC中，AC=BC，∠ACB=90°，D，E分别是BC，AC上一点，BD=AE，BE，AD交于M，
（1）求证：AM=BM；
（2）若∠BMD=45°，求$\frac{BM}{EM}$的值．
如图，△ABC中，AC=BC，∠ACB=90°，D，E分别是BC，AC上一点，BD=AE，BE，AD交于M，（1）求证：AM=BM；
（2）若∠BMD=45°，求$\frac{BM}{EM}$的值．
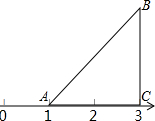如图，等腰直角三角形ABC的直角边AC落在数轴上，点A表示的数是1，点C表示的数是3，以A为旋转中心逆时针旋转△ABC．
如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG，垂足为E，BF⊥AG，垂足为F．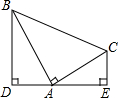
如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B、C作过点A的垂线BC、CE，垂足分别为D、E，若BD=3，CE=2，求DE的长．
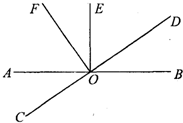如图，直线AB与CD相交于点D，OE⊥AB，OF⊥CD．
1．下列四种标志图案中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |