题目内容
3.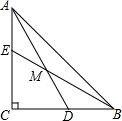 如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,(1)求证:AM=BM;
(2)若∠BMD=45°,求$\frac{BM}{EM}$的值.
分析 (1)由AB=AC,∠ACB=90°,得到△是等腰直角三角形,求得∠BAC=∠ABC=45°,通过△ABD≌△BAE,得到∠1=∠2,AD=BE,于是得到结论;
(2)过D作DF⊥AB于F,DN⊥BE于N,得到△BDF是等腰直角三角形,求出BD=$\sqrt{2}$DF,由(1)知,AD=BE,EM=DM,AM=BM,根据∠1=∠2,∠BMD=∠1+∠2=45°,于是得到∠1=∠2=22.5°求得△DCE是等腰直角三角形,于是得到DE=$\sqrt{2}$CD=BD,根据垂直平分线的性质得到BN=EN,推出△MDN是等腰直角三角形,求得EM=DM=$\sqrt{2}$MN,于是得到BN=EN=EM+MN=($\sqrt{2}$+1)MN,结论即可求得.
解答 解:(1)∵AB=AC,∠ACB=90°,
∴△是等腰直角三角形,
∴∠BAC=∠ABC=45°,
在△ABD与△BAE中,$\left\{\begin{array}{l}{BD=AE}\\{∠BAC=∠ABC}\\{AB=AB}\end{array}\right.$,
∴△ABD≌△BAE,
∴∠1=∠2,AD=BE,
∴AM=BM;
(2)过D作DF⊥AB于F,DN⊥BE于N,
∴△BDF是等腰直角三角形,
∴BD=$\sqrt{2}$DF,由(1)知,AD=BE,EM=DM,AM=BM,
∵∠1=∠2,∠BMD=∠1+∠2=45°,
∴∠1=∠2=22.5°,
∵∠BAC=∠ABC=45°,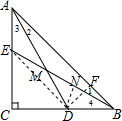
∴∠1=∠2=∠3=∠4=22.5°,
∴AD,BM分别平分∠BAC,∠ABC,
∴CD=DF,
∴BD=$\sqrt{2}$CD,
∴△DCE是等腰直角三角形,
∴DE=$\sqrt{2}$CD=BD,
∴DN是BE的垂直平分线,
∴BN=EN,
∵∠BMD=45°,
∴△MDN是等腰直角三角形,
∴EM=DM=$\sqrt{2}$MN,
∴BN=EN=EM+MN=($\sqrt{2}$+1)MN,
∴$\frac{BM}{EM}=\frac{BN+MN}{EN-MN}=\frac{(\sqrt{2}+1)MN+MN}{(\sqrt{2}+1)MN-MN}$=$\frac{\sqrt{2}+2}{\sqrt{2}}$=$\sqrt{2}+$1.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,线段的垂直平分线的性质,角平分线的性质,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案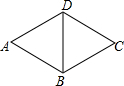 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
 如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )
如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
 的结果是( )
的结果是( )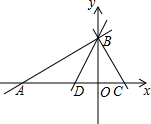 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根
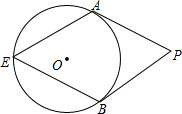 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.