题目内容
4.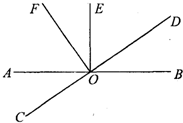 如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.(1)图中∠AOF的余角有∠EOF,∠AOC,∠BOD;(把符合条件的角都填出来)
(2)如果∠AOD=140°,那么根据对顶角相等,可得∠BOC=140度;
(3)∠EOF=$\frac{1}{5}$∠AOD,求∠EOF的度数.
分析 (1)根据余角的定义、性质,可得答案;
(2)根据对顶角的性质,可得答案;
(3)根据余角的性质,可得∠EOF与∠BOD的关系,根据平角的定义,可得答案.
解答 解:(1)图中∠AOF的余角有∠EOF,∠AOC,∠BOD;(把符合条件的角都填出来)
(2)如果∠AOD=140°,那么根据 对顶角相等,可得∠BOC=140度;
故答案为:∠EOF,∠AOC,∠BOD;对顶角相等,140;
(3)∵∠EOF+AOF=90°,∠AOC+∠AOF=90°,
∴∠EOF=∠AOC=∠BOD.
∵∠AOD+∠BOD=180°,∠EOF=$\frac{1}{5}$∠AOD
∴5∠EOF+∠BOD=180°,
即6∠EOF=180°,
∠EOF=30°.
点评 本题考查了对顶角、邻补角,利用了余角的性质,对顶角的性质,邻补角的性质.

练习册系列答案
相关题目
15.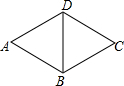 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
9.“a是有理数,|a|≥0”这一事件是( )
| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
13. 如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )
如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )
 如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )
如图,直线l1∥l2,∠1=35°,∠2=75°,则∠3等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
14.下列是因式分解的是( )
| A. | 4a2-4a+1=4a(a-1)+1 | B. | x2-4y2=(x+4y)(x-4y) | ||
| C. | x2+y2=(x+y)2 | D. | (xy)2-1=(xy+1)(xy-1) |
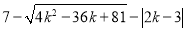 的结果是( )
的结果是( )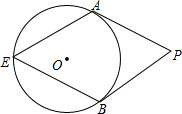 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度. 小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索
小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索