题目内容
20.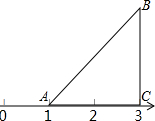 如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.
如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.(1)当旋转角度至少是135度时,点B的对应点落在数轴上;
(2)点B的对应点B1落在负半轴时,那么点B1所表示的数是-2$\sqrt{2}$+1.
分析 (1)利用等腰直角三角形的性质得到∠BAC=45°,由于以A为旋转中心逆时针旋转△ABC,所以旋转角度至少为135°时,点B的对应点落在数轴上;
(2)先利用点A和点C表示的数得AC=2,再根据等腰直角三角形的性质得AB=$\sqrt{2}$AC=2$\sqrt{2}$,再计算出OB1=AB1-OA=2$\sqrt{2}$-1,然后根据数轴表示数的方法求解.
解答  解:(1)∵△ABC为等腰直角三角形,
解:(1)∵△ABC为等腰直角三角形,
∴∠BAC=45°,
∴以A为旋转中心逆时针旋转△ABC,当旋转135°时,点B的对应点第一次落在数轴上;
(2)∵点A表示的数是1,点C表示的数是3,
∴AC=3-1=2,
∵△ABC为等腰直角三角形,
∴AB=$\sqrt{2}$AC=2$\sqrt{2}$,
∴OB1=AB1-OA=2$\sqrt{2}$-1,
∴点B1所表示的数为-2$\sqrt{2}$+1.
故答案为135,-2$\sqrt{2}$+1.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和实数与数轴.

练习册系列答案
相关题目
15.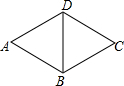 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
9.“a是有理数,|a|≥0”这一事件是( )
| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
10.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
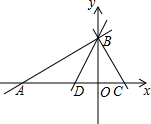 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+6与x轴相交于点A,与y轴相交于点B,过点B作直线BC⊥AB交x轴于点C,且OA和OC的长分别是方程x2+bx+c=0的两个根
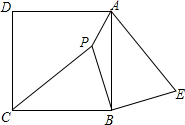 已知:如图,P是正方形ABCD内一点,△PCB顺时针旋转得到△ABE.
已知:如图,P是正方形ABCD内一点,△PCB顺时针旋转得到△ABE.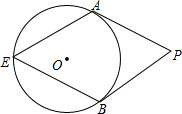 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.