题目内容
7. 如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG,垂足为E,BF⊥AG,垂足为F.
如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG,垂足为E,BF⊥AG,垂足为F.(1)求证:AE=BF;
(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求线段EF′的长.
分析 (1)由四边形ABCD是正方形,得AD=AB,∠DAG+∠BAF=90°,再由DE⊥AG,BF⊥AG,证得∠ADE=∠BAF,由AAS证得△ADE≌△BAF,即可得出结论;
(2)由旋转的性质得:∠AF′D=∠AFB=90°,∠DAF′=∠BAF,证明四边形AEDF′是矩形,即可得出EF′=AD=3.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,即∠DAG+∠BAF=90°,
∵DE⊥AG,BF⊥AG,
∴∠DEA=∠BFA=90°,
∴∠DAG+∠ADE=90°,
∴∠ADE=∠BAF,
在△ADE和△BAF中,$\left\{\begin{array}{l}{∠DEA=∠BFA}\\{∠ADE=∠BAF}\\{AD=AB}\end{array}\right.$,
∴△ADE≌△BAF(AAS),
∴AE=BF;
(2)解:如图所示: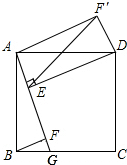
由旋转的性质得:∠AF′D=∠AFB=90°,∠DAF′=∠BAF,
∴∠F′AE=∠DAB=90°,
又∵∠DEA=90°
∴四边形AEDF′是矩形,
∴EF′=AD=3.
点评 本题考查了正方形的性质、旋转的性质、全等三角形的判定与性质、矩形的判定与性质;本题综合性强,有一定难度.

练习册系列答案
相关题目
15.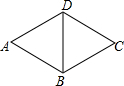 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
 如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )
如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,则可以作为旋转中心的点有( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
17.下列各组线段能组成一个三角形的是( )
| A. | 4cm,6cm,11cm | B. | 4cm,5cm,lcm | C. | 3cm,4cm,5cm | D. | 2cm,3cm,6cm |
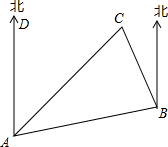 如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.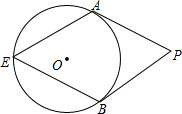 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度.
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠E=64°,则∠P=52度. 小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索
小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索