题目内容
20.解一元一次不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1>0}\\{2-x≥0}\end{array}\right.$,并在数轴上表示出它的解集.
分析 求出每个不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:$\left\{\begin{array}{l}{\frac{1}{3}x+1>0①}\\{2-x≥0②}\end{array}\right.$,
∵解不等式①,得x>-3,
解不等式②,得x≤2,
∴原不等式组的解集为:-3<x≤2,
数轴表示为: .
.
点评 本题考查了解一元一次不等式和一元一次不等式组的应用,关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
相关题目
11.一张试卷只有25道选择题,做对一题得4分,做错1题倒扣1分,某学生做了全部试题,得75分,他做对( )题.
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
15.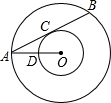 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 12 | B. | 6$\sqrt{3}$ | C. | 8 | D. | 3$\sqrt{3}$ |
5.下列图形:

其中是轴对称图形的共有( )

其中是轴对称图形的共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.若$\sqrt{x-1}$和$\sqrt{1-x}$在实数范围内都有意义,则x的取值是( )
| A. | x≥1 | B. | x≤1 | C. | x=1 | D. | -1≤x≤1 |
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=6,则CD的长为2.
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=6,则CD的长为2.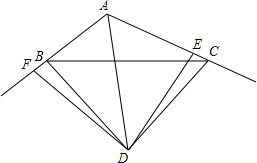 如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论:
如图,D为∠BAC的平分线上一点,BD=CD,过点D作DE⊥AC于E,DF⊥AB交AB的延长线于F,下列结论: