Question

15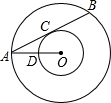．如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若OD=3，tan∠OAB=$\frac{1}{2}$，则AB的长是（　　）

• A． 12
• B． 6$\sqrt{3}$
• C． 8
• D． 3$\sqrt{3}$

Answer 1

分析 连接OC，利用切线的性质知OC⊥AB，由垂径定理得AB=2AC，因为tan∠OAB的值，易得OC：AC的值，进而可求出AC的长，而AB的长也可求出．

解答 解：连接OC，
∵大圆的弦AB切小圆于点C，
∴OC⊥AB，
∴AB=2AC，
∵OD=3，
∴OC=3，
∵tan∠OAB=$\frac{1}{2}$，
∴AC=6，
∴AB=12，
故选A．

点评 本题主要考查了切线的性质和垂径定理，连接过切点的半径是解答此题的关键．