题目内容
8.有六张正面分别标有数字-2,-1,0,1,2,3 的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,将该数字加1记为b.则数字a,b使得关于x的一元二次方程ax2+bx-1=0有解的概率为$\frac{1}{2}$.分析 根据题意可以求得a的取值范围,注意一元二次方程二次项系数不能为零,从而可以解答本题.
解答 解:由题意可得b=a+1,
∵关于x的一元二次方程ax2+bx-1=0有解,
∴b2-4a×(-1)=b2+4a=(a+1)2+4a≥0且a≠0,
解得a≤-3-2$\sqrt{2}$或a≥-3+2$\sqrt{2}$且a≠0,
∴数字a,b使得关于x的一元二次方程ax2+bx-1=0有解的概率为3÷6=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查概率公式、根的判别式,解答本题的关键是明确题意,求出相应的概率,二次项系数忽略,不能为零是易错点.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
16.等腰三角形的两边的长分别为2cm和7cm,则三角形的周长是( )
| A. | 11 | B. | 16 | C. | 11或16 | D. | 无法计算 |
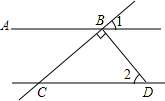 如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数.
如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数. 在如图网格中,A、B、M为格点,画线段MP⊥线段AB.
在如图网格中,A、B、M为格点,画线段MP⊥线段AB.