题目内容
8. 如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:
如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:①BC=AD;②AC平分∠BCD;③AC=AB;④∠ABC=∠ADC.
一定成立的是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ①② |
分析 根据全等三角形的判定和性质得出结论进而判断即可.
解答 解:∵点E是等腰三角形△ABD底边上的中点,
∴BE=DE,∠AEB=∠AED=90°,
∴∠BEC=∠DEC=90°,
在△BEC与△DEC中$\left\{\begin{array}{l}{BE=DE}\\{∠BEC=∠DEC}\\{EC=EC}\end{array}\right.$,
∴△BEC≌△DEC(SAS)
∴BC=CD,∠BCE=∠DCE,
∴∠ABC=∠ADC,
∴④∠ABC=∠ADC;②AC平分∠BCD正确,
故选C
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△BEC≌△DEC.

练习册系列答案
相关题目
7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=$\sqrt{3}$,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=$\sqrt{3}$,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=$\sqrt{3}$,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=$\sqrt{3}$,则折痕CE的长为( )| A. | 2 | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $2\sqrt{3}$ | D. | 3 |
16.下列说法正确的是( )
| A. | 无理数都是无限不循环小数 | B. | 有理数都是有限小数 | ||
| C. | 无限小数都是无理数 | D. | 带根号的数都是无理数 |
13.如果a>b,那么下列各式中正确的是( )
| A. | a-5<b-5 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | a+5<b+5 | D. | -3a<-3b |
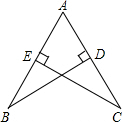 如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由.
如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由.