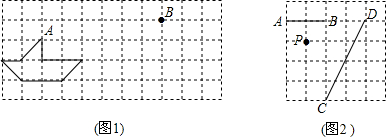题目内容
16．
如图所示，直线a∥b，AB⊥直线a，BC与直线b相交于点D，若∠1=43°，则∠2的度数是（ ）| A． | 43° | B． | 47° | C． | 120° | D． | 133° |
分析 先作辅助线延长AB交直线b于点F，再利用平行线的性质和三角形外角和内角的关系求角的度数．
解答 
解：延长AB交直线b于点F
∵a∥b，AB⊥a，
∴AB⊥b，
∴∠BFE=90°；
∵∠1=43°，∠2是三角形BEF的一个外角，
∴∠2=∠BFE+∠1=90°+43°=133°．
故选：D．
点评 本题考查了平行线的性质．构造三角形是常用的作辅助线的方法．
练习册系列答案
相关题目
6．下列图形中，绕着某一点旋转180°后能与它本身完全重合的是（ ）
| A． | 平行四边形 | B． | 等边三角形 | C． | 等腰直角三角形 | D． | 抛物线 |
7．下列数中，是有理数的是（ ）
| A． | π | B． | （-2$\sqrt{3}$）2 | C． | $\sqrt{2}$ | D． | $\root{3}{9}$ |
4．
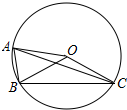如图，⊙O是△ABC的外接圆，∠BOC=3∠AOB，若∠ACB=20°，则∠BAC的度数是（ ）
如图，⊙O是△ABC的外接圆，∠BOC=3∠AOB，若∠ACB=20°，则∠BAC的度数是（ ）| A． | 120° | B． | 80° | C． | 60° | D． | 30° |
