题目内容
6.下列图形中,绕着某一点旋转180°后能与它本身完全重合的是( )| A. | 平行四边形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 抛物线 |
分析 把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,然后选出中心对称图形即可.
解答 解:平行四边形绕着某一点旋转180°后能与它本身完全重合,
故选:A.
点评 此题主要考查了中心对称图形,关键是掌握中心对称图形的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{4\sqrt{13}}{13}$ |
17.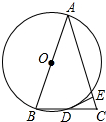 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB=$\frac{12}{13}$,求CE的长.
 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB=$\frac{12}{13}$,求CE的长.
1.等腰直角三角形的斜边长为a,则其斜边上的高为( )
| A. | $\frac{a}{2}$ | B. | $\sqrt{2}a$ | C. | $\frac{\sqrt{3}}{2}$a | D. | $\frac{\sqrt{2}}{4}$a |
16. 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )| A. | 43° | B. | 47° | C. | 120° | D. | 133° |
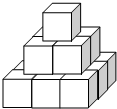 如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.
如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.