题目内容
6.如果k是数据2,5,3,8,8中的中位数,求关于x的方程$\frac{1-x}{2x-1}$+$\frac{k}{1-2x}$=1的解.分析 根据中位数,可得k值,根据等式的性质,可得整式方程,根据解整式方程,可得方程的解.
解答 解:由题意得k=5.
原方程变为$\frac{1-x}{2x-1}$-$\frac{5}{2x-1}$=1.
去分母,得1-x-5=2x-1
移项,合并得-3x=3
x=-1,
经检验:x=-1是原方程式的解.
点评 本题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,解分式方程一定注意要验根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )| A. | 43° | B. | 47° | C. | 120° | D. | 133° |
17.在一个已经装有10个黑色玻璃球的不透明布袋中再装入30个红色、白色玻璃球,这些球除颜色外其他完全相同.小花做摸球实验,她将袋子里面的球充分搅均匀后从中随机摸出一个球记下颜色,再把它放回袋子里,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 67 | 122 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.67 | 0.61 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
11.直线y=(1-2m)x+m-1,不论m取什么值,该直线必定经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.某公园中央地上有一个大理石球,小明想测量球的半径,于是找了两块厚20cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是80cm,聪明的你,请你算出大石头的半径是( )


| A. | 40cm | B. | 30cm | C. | 20cm | D. | 50cm |
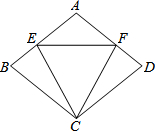 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等. 雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.
雾霾成为“两会”最大的民生话题. 浙江2015年十件民生实事已公布,雾霾治理居首位,杭州市确定了7600亿元的巨额治理投资,将用市场手段治理雾霾.7600亿元,用科学记数法表示为7.6×1011元.