题目内容
1．
小明动手操作如下，先剪一个等腰三角形纸片ABC，使AB=AC，再把∠B沿EM折叠，使点B落在点D上；把∠C沿FN折叠，使点C落在点D上，则四边形AEDF是平行四边形，你认为正确吗？请说明理由．
分析 四边形AEDF是平行四边形，可证明DE∥AC，DF∥AB即可．
解答 证明：四边形AEDF是平行四边形；理由如下：
∵AB=AC，
∴∠B=∠C，
根据折叠的性质，∠B=∠BDE，∠C=∠CDF
∴∠B=∠CDF，∠C=∠BDE，
∴DF∥AB，DE∥AC，
∴四边形AEDF是平行四边形；
点评 本题主要考查了折叠变换的性质、平行四边形的判定、等腰三角形的性质；熟练掌握折叠变换的性质，证出DF∥AB，DE∥AC是解决问题的关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
6．下列运算正确的是（ ）
| A． | a3•a2=a6 | B． | 3-1=-3 | C． | （-2a）3=-8a3 | D． | 20160=0 |
12．已知一次函数y=kx+b，k，b从-1，-2，3中随机取一个值，则该函数图象经过一、二、四象限的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{9}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{6}$ |
16．将四个编号为1，2，3，4的小球随机放入4个编号为1，2，3，4的盒子中．记f（i）为第i个盒子中小球的编号与盒子编号的差的绝对值．则f（1）+f（2）+f（3）+f（4）=4的概率为（ ）
| A． | $\frac{5}{16}$ | B． | $\frac{5}{24}$ | C． | $\frac{1}{4}$ | D． | $\frac{7}{24}$ |
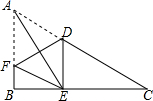如图，在△ABC中，∠B=90°，点D在AC边上，DE⊥BC于E，将△ABC沿过点D的直线对折，使点A落在BC边上的点E处，折痕交AB于点F．