题目内容
12.已知一次函数y=kx+b,k,b从-1,-2,3中随机取一个值,则该函数图象经过一、二、四象限的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
分析 先画树状图展示所有6种等可能的结果数,然后根据已次函数的性质找出满足k<0,b>0的结果数,再利用概率公式求解.
解答 解:当k<0,b>0时,函数图象经过一、二、四象限,
画树状图为:
共有6种等可能的结果数,其中满足k<0,b>0的结果数为2,
所以该函数图象经过一、二、四象限的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故选A.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果数n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求解.也考查了一次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列计算正确的是( )
| A. | x+x2=x3 | B. | x2•x3=x6 | C. | (x3)2=x6 | D. | x6÷x3=x2 |
18.已知∠1=42°45′,则∠1的余角等于( )
| A. | 47°55′ | B. | 47°15′ | C. | 48°15′ | D. | 137°55′ |
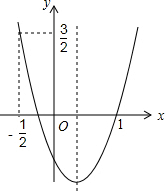 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.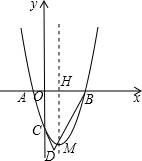 如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.
如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.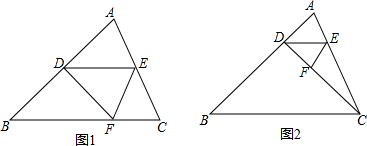
 小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.
小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.