题目内容
17.已知x为实数,且满足(x2+x+1)2+2(x2+x+1)-3=0,那么x2+x+1的值为( )| A. | 1 | B. | -3 | C. | -3或1 | D. | -1或3 |
分析 首先利用换元思想,把x2+x+1看做一个整体换为y,化为含y一元二次方程,解这个方程,再检验即可.
解答 解:设y=x2+x+1=y,
则(x2+x+1)2+2(x2+x+1)-3=0,可化为:y2+2y-3=0,
分解因式得:(y+3)(y-1)=0,
解得:y1=-3,y2=1,
当x2+x+1=-3时,经△=12-4×1×4<0检验,可知x不是实数,
当x2+x+1=1时,经检验,符合题意.
故选A.
点评 此题考查了用换元法解一元二次方程,考察了学生的整体思想.解题的关键是找到哪个是换元的整体.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2.已知小明上学时,走上坡路,速度为m千米/时;放学回家时,沿原路返回,速度为n千米/时,则小明上学和放学时的平均速度为( )
| A. | $\frac{m+n}{2}$千米/时 | B. | $\frac{mn}{m+n}$千米/时 | C. | $\frac{2mn}{m+n}$千米/时 | D. | $\frac{m+n}{mn}$千米/时 |
7.一个正数的平方根是x-5和x+1,则x的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | 无法确定 |
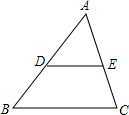 如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.
如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.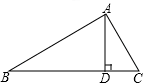 如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.
如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.