题目内容
2．已知小明上学时，走上坡路，速度为m千米/时；放学回家时，沿原路返回，速度为n千米/时，则小明上学和放学时的平均速度为（ ）| A． | $\frac{m+n}{2}$千米/时 | B． | $\frac{mn}{m+n}$千米/时 | C． | $\frac{2mn}{m+n}$千米/时 | D． | $\frac{m+n}{mn}$千米/时 |
分析 设从家到学校的单程为1，那么总路程为2，根据平均速度=$\frac{总路程}{总时间}$，列分式并化简即可得出答案．
解答 解：设上学路程为1，则往返总路程为2，上坡时间为$\frac{1}{m}$，下坡时间为$\frac{1}{n}$，
则平均速度=$\frac{2}{\frac{1}{m}+\frac{1}{n}}$=$\frac{2mn}{m+n}$（千米/时）．
故选C
点评 本题考查了列代数式以及平均数的求法，用到的知识点是平均速度=$\frac{总路程}{总时间}$，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量关系．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12．
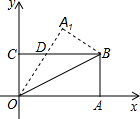如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）
如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）| A． | （$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$） | B． | （$\frac{{\sqrt{3}}}{2}$，$\frac{3}{2}$） | C． | （$\frac{{\sqrt{3}}}{2}$，2） | D． | （$\frac{3}{2}$，$\frac{{\sqrt{3}}}{2}$） |
17．已知x为实数，且满足（x2+x+1）2+2（x2+x+1）-3=0，那么x2+x+1的值为（ ）
| A． | 1 | B． | -3 | C． | -3或1 | D． | -1或3 |
如图，在?ABCD中，DE⊥AB于点E，DF⊥BC于点F，且∠ADE+∠CDF=60°，求∠EDF的度数60°．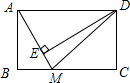
如图，矩形ABCD中，AB=4，AD=9，点M在BC上，且BM：MC=1：2，DE⊥AM于点E，求DE的长为$\frac{36}{5}$．
如图，把一根底面半径为2dm，高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块，每块木料的表面积是多少平方分米？