题目内容
12.已知不等臂跷跷板AB长为4米,如图1,当AB的一端A碰到地面时,AB与地面的夹角为α,如图2,当AB的另一端B碰到地面时,AB与地面的夹角为β,已知α=30°,β=37°,求跷跷板AB的支撑点O到地面的高度OH(sin37°=0.6,cos37°=0.8,tan37°=0.75).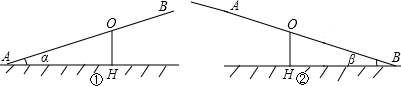
分析 根据三角函数的知识分别用OH表示出AO,BO的长,再根据不等臂跷跷板AB长4米,即可列出方程求解即可.
解答 解:根据题意得:AO=OH÷sinα,BO=OH÷sinβ,
AO+BO=OH÷sinα+OH÷sinβ,
即OH÷sinα+OH÷sinβ=4,
则OH=$\frac{4sinα•sinβ}{sinα+sinβ}$=$\frac{4×sin30°×sin37°}{sin30°+sin37°}$=$\frac{4×\frac{1}{2}×0.6}{\frac{1}{2}+0.6}$=$\frac{12}{11}$(米).
即故跷跷板AB的支撑点O到地面的高度OH是$\frac{12}{11}$米.
点评 本题考查的是解直角三角形的应用,根据题意利用锐角三角函数的定义得出求OH的关系式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|=( )
| A. | a+b+c | B. | -a+3b-c | C. | a+b-c | D. | 2b-2c |
7.不等式组$\left\{\begin{array}{l}x>-2\\ x>a.\end{array}\right.$的解集是x>a,则a的取值范围是( )
| A. | a<-2 | B. | a=-2 | C. | a>-2 | D. | a≥-2 |
17.已知x为实数,且满足(x2+x+1)2+2(x2+x+1)-3=0,那么x2+x+1的值为( )
| A. | 1 | B. | -3 | C. | -3或1 | D. | -1或3 |
4.如图图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |