题目内容

9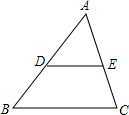．如图，在△ABC中，D、E分别为AB、AC的中点，连接DE，若S△ADE=2，则四边形BDEC的面积为6．

分析 依据三角形的中位线定理得出DE∥BC，DE=$\frac{1}{2}$BC，然后根据三角形面积的比等于相似比的平方即可取得三角形ABC的面积，用三角形ABC的面积减去三角形ADE的面积即可．

解答 解：∵D、E分别是AB、AC的中点，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴∠ADE=∠B，∠AED=∠C，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{DE}{BC}$）2=（$\frac{1}{2}$）2=$\frac{1}{4}$，
∵S△ADE=2，
∴S△ABC=4S△ADE=4×2=8．
∴S四边形DECB=S△ABC-S△ADE=8-2=6．
故答案为6．

点评 本题考查了三角形的中位线定理的应用，以及相似三角形的判定和性质，熟记相似三角形的面积的比等于相似比的平方是解题关键．

练习册系列答案
相关题目
19．阅读下列材料，并解答问题：
材料：将分式$\frac{{{x^2}-x+3}}{x+1}$拆分成一个整式与一个分式（分子为整数）的和的形式．
解：由分母x+1，可设x2-x+3=（x+1）（x+a）+b
则x2-x+3=（x+1）（x+a）+b=x2+ax+x+a+b=x2+（a+1）x+a+b
∵对于任意x上述等式成立
∴$\left\{\begin{array}{l}a+1=-1\\ a+b=3\end{array}\right.$解得：$\left\{\begin{array}{l}a=-2\\ b=5\end{array}\right.$
∴$\frac{{{x^2}-x+3}}{x+1}=\frac{（x+1）（x-2）+5}{x+1}=x-2+\frac{5}{x+1}$
这样，分式$\frac{{{x^2}-x+3}}{x+1}$就拆分成一个整式x-2与一个分式$\frac{5}{x+1}$的和的形式．
（1）将分式$\frac{{{x^2}+6x-3}}{x-1}$拆分成一个整式与一个分式（分子为整数）的和的形式为$x+7+\frac{4}{x-1}$；
（2）已知整数x使分式$\frac{{2{x^2}+5x-20}}{x-3}$的值为整数，则满足条件的整数x=4、16、2、-10；
（3）当-1＜x＜1时，求分式$\frac{{{x^4}+3{x^2}-2}}{{{x^2}+1}}$的最小值．
20．若a、b、c是△ABC的三边的长，则化简|a-b-c|-|b-c-a|+|a+b-c|=（　　）
A．a+b+cB．-a+3b-cC．a+b-cD．2b-2c
17．已知x为实数，且满足（x2+x+1）2+2（x2+x+1）-3=0，那么x2+x+1的值为（　　）
A．1B．-3C．-3或1D．-1或3
4．如图图形中，既是轴对称图形，又是中心对称图形的是（　　）
A．B．C．D．
14．如图，在?ABCD中，DE⊥AB于点E，DF⊥BC于点F，且∠ADE+∠CDF=60°，求∠EDF的度数60°．
1．$\root{3}{-8}$等于-2．
18．如图1，正方形ABCD中，点E为AD上任意一点，连接BE，以BE为边向BE右侧作正方形BEFG，EF交CD于点M，连接BM，N为BM的中点，连接GN，FN．
（1）若AB=4，AE：DE=3：1，求EM的长；
（2）求证：GN=FN；
（3）如图2，移动点E，使得FN⊥CD于点Q时，请探究CM与DE的数量关系并说明理由．
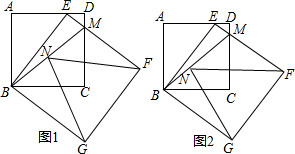
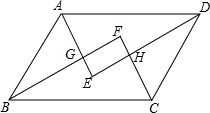19．?ABCD中，AE、CF、BF、DE分别为四个内角平分线，求证：EGFH是矩形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网