题目内容
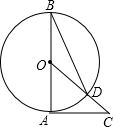 已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数.
已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数.考点:切线的性质
专题:计算题
分析:先根据切线的性质得∠OAC=90°,再利用互余计算出∠AOC=90°-∠C=50°,由于∠OBD=∠ODB,利用三角形的外角性质得∠OBD=
∠AOC=25°.
| 1 |
| 2 |
解答:解:∵AC是⊙O的切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∵OB=OD,
∴∠OBD=∠ODB,
而∠AOC=∠OBD+∠ODB,
∴∠OBD=
∠AOC=25°,
即∠ABD的度数为25°.
∴OA⊥AC,
∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∵OB=OD,
∴∠OBD=∠ODB,
而∠AOC=∠OBD+∠ODB,
∴∠OBD=
| 1 |
| 2 |
即∠ABD的度数为25°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
校、家、书店依次坐落在一条南北走向的大街上,学校在家南边20米,书店在家北边100米,张明从家里出发,向北走了40米,接着又向南走了-60米,此时张明的位置在( )
| A、在家 | B、在学校 |
| C、在书店 | D、不在上述地方 |
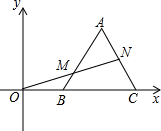 如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为
如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为