题目内容
20. 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.
分析 根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≌Rt△EBD,从而得出DF=BD.
解答 证明:∵AD是∠BAC的平分线,DE⊥AB于E,DC⊥AC于C,
∴DE=DC.
在Rt△CDF和Rt△EDB中,
$\left\{\begin{array}{l}{DC=DE}\\{∠C=∠DEB}\\{CF=BE}\end{array}\right.$
∴Rt△CDF≌Rt△EDB(SAS),
∴DF=BD.
点评 本题主要考查角平分线的性质,全等三角形的判定与性质.求得CD=DE是解答本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.已知a,b是一元二次方程x2+2x-9=0的两根,则a2+a-b的值等于( )
| A. | 7 | B. | 11 | C. | -7 | D. | -11 |
10.以下各图中,能确定∠1=∠2的是( )
| A. |  | B. |  | C. |  | D. |  |
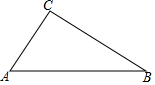 如图,Rt△ABC中,∠C=Rt∠,AC=6,BC=8,点D在BC上,D到AB的距离等于CD.
如图,Rt△ABC中,∠C=Rt∠,AC=6,BC=8,点D在BC上,D到AB的距离等于CD. 如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.
如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.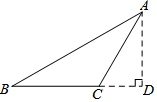 如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.
如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.