题目内容
17.已知二次函数y=x2+(2m-1)x,当x<0时,y随x的增大而减小,则m的取值范围是m$≤\frac{1}{2}$.分析 先根据二次函数的解析式判断出函数的开口方向,再由当x>4时,函数值y随x的增大而减小可知二次函数的对称轴x=-$\frac{b}{2a}$≥0,故可得出关于m的不等式,求出m的取值范围即可.
解答 解:∵二次函数y=x2+(2m-1)x中,a=1>0,
∴此函数开口向上,
∵当x<0时,y随x的增大而减小,
∴二次函数的对称轴x=-$\frac{b}{2a}$≥0,即m$≤\frac{1}{2}$,
故答案为:m$≤\frac{1}{2}$.
点评 本题考查的是二次函数的性质,熟知二次函数的增减性是解答此题的关键.

练习册系列答案
相关题目
5. 如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
 如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )| A. | 点O1 | B. | 点O2 | C. | 点O3 | D. | 点O4 |
2.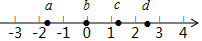 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
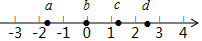 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
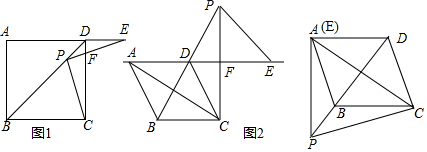
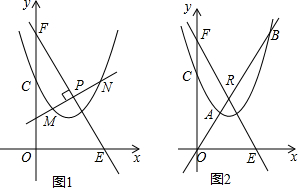
 数轴上点A表示的分数是:$\frac{7}{3}$.
数轴上点A表示的分数是:$\frac{7}{3}$. 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.