题目内容
5.材料:一般地,n个相同因数a相乘:$\underset{\underbrace{a•a•a…a•a}}{n个}$记为an.如23=8,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=2,(log216)2+$\frac{1}{3}$log327=17.
分析 想一想3的几次方等于9?故此可得到log39的值,然后再求得log216和log327的值,最后依据有理数的运算法则进行计算即可.
解答 解:∵32=9,
∴log39=2.
∵24=16,
∴log216=4.
∵33=27,
∴log327=3
∴(log216)2+$\frac{1}{3}$log327=42+$\frac{1}{3}$×3=17.
故答案为:2;17.
点评 本题主要考查的是定义新运算,读懂题意,掌握运算方法是解题的关键.

练习册系列答案
相关题目
2.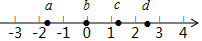 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
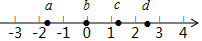 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
10.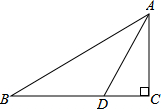 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
14.下列运算正确的是( )
| A. | a5•a3=a9 | B. | a2÷a=a | C. | 3a-a=3 | D. | (3a)2=6a2 |
15.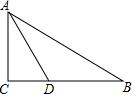 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
 如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$.
如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$. 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF. 如图,请按下列要求画图:
如图,请按下列要求画图: