题目内容
8.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)均是反比例函数y=$\frac{-3}{x}$图象上点,且有x1<x2<0<x3,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y3<y1<y2 |
分析 根据反比例函数图象上点的坐标特征得到y1=$\frac{-3}{{x}_{1}}$,y2=$\frac{-3}{{x}_{2}}$,y3=$\frac{-3}{{x}_{3}}$,然后根据自变量的大小比较y1,y2,y3的大小.
解答 解:∵P1(x1,y1),P2(x2,y2),P3(x3,y3)均是反比例函数y=$\frac{-3}{x}$图象上点,
∴y1=$\frac{-3}{{x}_{1}}$,y2=$\frac{-3}{{x}_{2}}$,y3=$\frac{-3}{{x}_{3}}$,
而x1<x2<0<x3,
∴y3<y2<y1.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19.在下列实数中:$\sqrt{5}$,$\root{3}{π^3}$,3.01001000100001…,$\sqrt{16}$,$\frac{22}{7}$,$\root{3}{-9}$,无理数的个数( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.下列条件中,不能判断四边形ABCD是平行四边形的是( )
| A. | AB=CD,AD∥BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD=BC | D. | AB∥CD,AD∥BC |
3.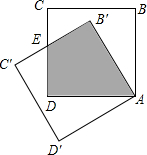 如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
 如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )| A. | 1-$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 1-$\frac{2\sqrt{3}}{3}$ |
13.要调查我校初中7000多名学生的视力情况,下列调查方式最合适的是( )
| A. | 在我校初一年级学生中随机选取100名女生 | |
| B. | 在我校初二年级学生中随机选取100名男生 | |
| C. | 在我校初三年级学生中随机选取100名学生 | |
| D. | 在我校7000多名初中学生中随机选取100名学生 |
 如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.
如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.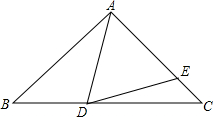 如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.
如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°. 如图,在矩形ABCD中,以BC边为直径的半圆交AD边于点P,连结PB、PC.若∠PBC=35°,则∠PCD为55度.
如图,在矩形ABCD中,以BC边为直径的半圆交AD边于点P,连结PB、PC.若∠PBC=35°,则∠PCD为55度.