题目内容
18. 如图,在矩形ABCD中,以BC边为直径的半圆交AD边于点P,连结PB、PC.若∠PBC=35°,则∠PCD为55度.
如图,在矩形ABCD中,以BC边为直径的半圆交AD边于点P,连结PB、PC.若∠PBC=35°,则∠PCD为55度.
分析 根据圆周角定理得到∠BPC=90°,然后利用互余计算∠PCD的度数.
解答 解:∵BC边为直径,
∴∠BPC=90°,
∴∠PCD=90°-∠PBC=90°-35°=55°.
故答案为55°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)均是反比例函数y=$\frac{-3}{x}$图象上点,且有x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y3<y1<y2 |
6.三角形的重心是指( )
| A. | 三边高的交点 | B. | 三角角平分线的交点 | ||
| C. | 三边中线的交点 | D. | 三边中垂线的交点 |
20.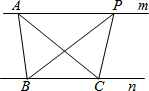 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )| A. | AB∥PC | B. | △ABC的面积等于△BCP的面积 | ||
| C. | AC=BP | D. | △ABC的周长等于△BCP的周长 |




 如图,已知线段AB=20厘米,M是AB的中点,P在MB上,N为PB的中点,NB=4厘米,则PM=2厘米.
如图,已知线段AB=20厘米,M是AB的中点,P在MB上,N为PB的中点,NB=4厘米,则PM=2厘米.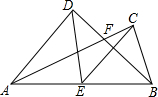 如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点,
如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点, 填空题:
填空题: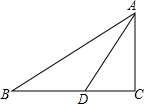 如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AD=$\sqrt{5}$,∠CAD=∠ABC=α,且tanα=$\frac{1}{2}$,则BD的长为( )
如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AD=$\sqrt{5}$,∠CAD=∠ABC=α,且tanα=$\frac{1}{2}$,则BD的长为( )