Question

3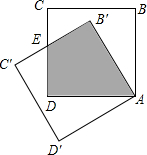．如图，边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′，则图中阴影部分面积为（　　）

• A． 1-$\frac{\sqrt{3}}{3}$
• B． $\frac{\sqrt{3}}{3}$
• C． $\frac{2\sqrt{3}}{3}$
• D． 1-$\frac{2\sqrt{3}}{3}$

Answer 1

分析 连接AE．根据HL易证△AB′E≌△ADE，得出∠B′AE=∠DAE=30°．在直角△ADE中，由正切的定义得出DE=AD•tan∠DAE=$\frac{\sqrt{3}}{3}$．再利用三角形的面积公式求出S_{四边形AB′ED}=2S_△ADE．

解答 解：设B′C′与CD交于点E，连接AE．
在△AB′E与△ADE中，∠AB′E=∠ADE=90°，
∵$\left\{\begin{array}{l}{AE=AE}\\{AB′=AD}\end{array}\right.$，
∴△AB′E≌△ADE（HL），
∴∠B′AE=∠DAE．
∵∠BAB′=30°，∠BAD=90°，
∴∠B′AE=∠DAE=30°，
∴DE=AD•tan∠DAE=$\frac{\sqrt{3}}{3}$．
∴S_{四边形AB′ED}=2S_△ADE=2×$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$，
故选B．

点评 本题主要考查了正方形、旋转的性质，直角三角形的判定及性质，图形的面积以及三角函数等知识，综合性较强，有一定难度．