题目内容
 阅读下面的材料:
阅读下面的材料:(1)锐角三角函数概念:在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,称sinA=
| a |
| c |
| b |
| c |
| c |
| c |
由sinA=
| a |
| c |
| a |
| sinA |
| b |
| c |
| b |
| sinB |
而c=
| c |
| 1 |
| c |
| sin90° |
| c |
| sinC |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
(2)其实,对于任意的锐角△ABC,上述结论仍然成立,即三角形各边与对角的正弦之比相等,我们称之为“正弦定理”,我们可以利用三角形面积公式证明其正确性.
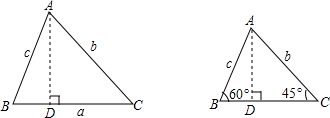
证明:如图1作AD⊥BC于D则在Rt△ABD中,sinB=
| AD |
| c |
∴AD=c•sinB,∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ACD中,sinC=
| AD |
| b |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因此有S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
也就是=ac•sinB=ab•sinC=bc•sinA.
每项都除以abc,得
| sinB |
| b |
| sinC |
| c |
| sinA |
| a |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
请你根据对上面材料的理解,解答下列问题:
(1)在锐角△ABC中,∠B=60°,∠C=45°,c=2,求b;
(2)求问题(1)中△ABC的面积;
(3)求sin75°的值(以上均求精确值,结果带根号的保留根号)
考点:解直角三角形
专题:阅读型
分析:(1)根据阅读材料得到
=
=
,则
=
,可计算出b=
;
(2)作AD⊥BC于D,如图,在Rt△ABD中,利用余弦的定义得cosB=cos60°=
,可计算出BD=1,在Rt△ADC中,根据等腰直角三角形的性质得AD=CD=
AC=
,所以BC=BD+CD=
+1,然后根据三角形面积公式计算得到△ABC的面积=
;
(3)先根据三角形内角和定理得到∠A=180°-∠B-∠C=75°,再根据阅读材料得到△ABC的面积=
bcsinA,即
•
•2•sin75°=
,可计算出sin75°=
.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| b |
| sin60° |
| 2 |
| sin45° |
| 6 |
(2)作AD⊥BC于D,如图,在Rt△ABD中,利用余弦的定义得cosB=cos60°=
| BD |
| AB |
| ||
| 2 |
| 3 |
| 3 |
3+
| ||
| 2 |
(3)先根据三角形内角和定理得到∠A=180°-∠B-∠C=75°,再根据阅读材料得到△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
3+
| ||
| 2 |
| ||||
| 4 |
解答:解:(1)∵
=
=
,
∴
=
,
∴b=
=
;
(2)作AD⊥BC于D,如图,
在Rt△ABD中,cosB=cos60°=
=
,
∴BD=1,
在Rt△ADC中,AD=CD=
AC=
×
=
,
∴BC=BD+CD=
+1,
∴△ABC的面积=
×
×(
+1)=
;
(3)∵∠B=60°,∠C=45°,
∴∠A=180°-∠B-∠C=75°,
∴△ABC的面积=
bcsinA,
∴
•
•2•sin75°=
,
∴sin75°=
.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴
| b |
| sin60° |
| 2 |
| sin45° |
∴b=
2×
| ||||
|
| 6 |

(2)作AD⊥BC于D,如图,
在Rt△ABD中,cosB=cos60°=
| BD |
| AB |
| BD |
| 2 |
∴BD=1,
在Rt△ADC中,AD=CD=
| ||
| 2 |
| ||
| 2 |
| 6 |
| 3 |
∴BC=BD+CD=
| 3 |
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
| 3 |
3+
| ||
| 2 |
(3)∵∠B=60°,∠C=45°,
∴∠A=180°-∠B-∠C=75°,
∴△ABC的面积=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 6 |
3+
| ||
| 2 |
∴sin75°=
| ||||
| 4 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
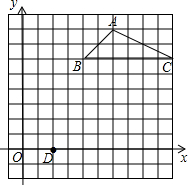 作图题:我们把顶点在正方形网格交点上的图形叫做格点图形,如图,△ABC就是一个格点三角形,图中的正方形网格边长为1个单位长度.
作图题:我们把顶点在正方形网格交点上的图形叫做格点图形,如图,△ABC就是一个格点三角形,图中的正方形网格边长为1个单位长度.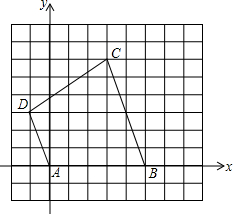 如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.
如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD. 如图,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.
如图,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.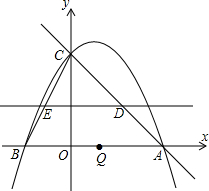 如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).
如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).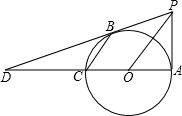 如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.
如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.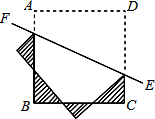 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为
如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为