题目内容
为响应“大课间”活动,某学校准备购买棒球和篮球共200个,已知棒球每个55元,篮球每个95元,学校计划至少投入资金18200元,但不多于18300元.
(1)学校有多少种购买方案;
(2)哪种购买方案使学校投入资金最少?
(3)当学校按(2)的方案买回200个球在“大课间”投入使用后,学校领导根据实际情况发现还应同时购买足球和大绳若干,来补充“大课间”活动,所以又投入资金2880元,若每个足球80元,每条大绳30元,则在钱全部用尽的情况下有多少种购买方法,请直接写出购买方法的种数.
(1)学校有多少种购买方案;
(2)哪种购买方案使学校投入资金最少?
(3)当学校按(2)的方案买回200个球在“大课间”投入使用后,学校领导根据实际情况发现还应同时购买足球和大绳若干,来补充“大课间”活动,所以又投入资金2880元,若每个足球80元,每条大绳30元,则在钱全部用尽的情况下有多少种购买方法,请直接写出购买方法的种数.
考点:一元一次不等式组的应用
专题:
分析:(1)设购买棒球x个,则购买篮球(200-x)个,根据总价等于两种球的价格之和建立不等式组求出其解即可;
(2)设学校的总投资为W元,根据总投资等于两种球的价格之和就可以表示出W与x的关系式,由一次函数的解析式就可以求出结论;
(3)设足球买a个,大绳b个,根据足球的费用+大绳的费用之和=2880元建立方程,解一个不定方程即可.
(2)设学校的总投资为W元,根据总投资等于两种球的价格之和就可以表示出W与x的关系式,由一次函数的解析式就可以求出结论;
(3)设足球买a个,大绳b个,根据足球的费用+大绳的费用之和=2880元建立方程,解一个不定方程即可.
解答:解:(1)设购买棒球x个,则购买篮球(200-x)个,由题意,得
,
解得:17.5≤x≤20.
∵x为整数,
∴x=18,19,20.
∴购买方案有3种:
方案1,买棒球18个,买篮球182个,
方案2,买棒球19个,买篮球181个,
方案3,买棒球20个,买篮球180个,
(2)设学校的总投资为W元,由题意,得
W=55x+95(200-x)=-40x+19000,
∴k=-40<0,
∴W随x的增大而减小,
∴当x=20时,w最小=18200;
(3)设足球买a个,大绳b条,由题意,得
80a+30b=2880,
a=
,
∵a≥0,b≥0,
≥0,
∴b≤96.
∵80a≤2880,
∴a≤36,
∵a,b为整数,
∴288-3b是8的倍数,
∴3b是24的倍数,
∴288-3b=0,24,48,72,96,120,144,168,192,216,240,264,288,
∴b=96,88,80,72,64,56,48,40,32,24,16,8,0,
∴a=0,3,6,9,12,15,18,21,24.27,30,33,36,
∴共有12种购买方法:
1,足球买0个,大绳96条,
2,足球买3个,大绳88条,
3,足球买6个,大绳80条,
4,足球买9个,大绳72条,
5,足球买12个,大绳64条,
6,足球买15个,大绳56条,
7,足球买18个,大绳48条,
8,足球买21个,大绳40条,
9,足球买24个,大绳32条,
10,足球买27个,大绳24条,
11,足球买30个,大绳16条,
12,足球买33个,大绳8条,
13,足球买36个,大绳0条.
|
解得:17.5≤x≤20.
∵x为整数,
∴x=18,19,20.
∴购买方案有3种:
方案1,买棒球18个,买篮球182个,
方案2,买棒球19个,买篮球181个,
方案3,买棒球20个,买篮球180个,
(2)设学校的总投资为W元,由题意,得
W=55x+95(200-x)=-40x+19000,
∴k=-40<0,
∴W随x的增大而减小,
∴当x=20时,w最小=18200;
(3)设足球买a个,大绳b条,由题意,得
80a+30b=2880,
a=
| 288-3b |
| 8 |
∵a≥0,b≥0,
| 288-3b |
| 8 |
∴b≤96.
∵80a≤2880,
∴a≤36,
∵a,b为整数,
∴288-3b是8的倍数,
∴3b是24的倍数,
∴288-3b=0,24,48,72,96,120,144,168,192,216,240,264,288,
∴b=96,88,80,72,64,56,48,40,32,24,16,8,0,
∴a=0,3,6,9,12,15,18,21,24.27,30,33,36,
∴共有12种购买方法:
1,足球买0个,大绳96条,
2,足球买3个,大绳88条,
3,足球买6个,大绳80条,
4,足球买9个,大绳72条,
5,足球买12个,大绳64条,
6,足球买15个,大绳56条,
7,足球买18个,大绳48条,
8,足球买21个,大绳40条,
9,足球买24个,大绳32条,
10,足球买27个,大绳24条,
11,足球买30个,大绳16条,
12,足球买33个,大绳8条,
13,足球买36个,大绳0条.
点评:本题考查了一元一次不等式组的解法的运用,方案设计的运用,一次函数的解析式的性质的运用,二元一次不定方程的解法的运用,解答时建立解析式是关键,解答不定方程是难点.

练习册系列答案
相关题目
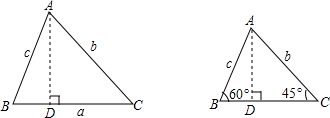 阅读下面的材料:
阅读下面的材料: 如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为
如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为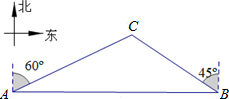 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里,
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里, 如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°. 如图,在平面直角坐标系中,AB∥OC,A(0,12),B(21,12),C(16,0).一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒).
如图,在平面直角坐标系中,AB∥OC,A(0,12),B(21,12),C(16,0).一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒).