题目内容
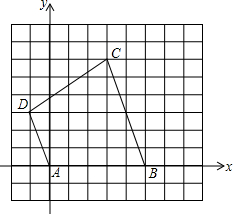 如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.
如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.(1)请判断四边形ABCD的形状,并求出四边形ABCD的面积.
(2)在所给的在10×10的正方形网格纸中画出到AB和CD所在直线的距离相等的所有网格点P,并直接写出点P的坐标.(不需说明理由)
考点:坐标与图形性质,三角形的面积,角平分线的性质
专题:
分析:(1)根据网格结构判断出AD∥BC,然后根据梯形的定义判断即可,再根据梯形的面积等于一个三角形的面积加上平行四边形的面积列式计算即可得解;
(2)根据角平分线上的点到角的两边距离相等,∠B=∠C作出BC的垂直平分线,所经过的格点即为所求的点.
(2)根据角平分线上的点到角的两边距离相等,∠B=∠C作出BC的垂直平分线,所经过的格点即为所求的点.
解答:解:(1)四边形ABCD是梯形,
四边形ABCD的面积=
×5×3+5×3=7.5+15=22.5;
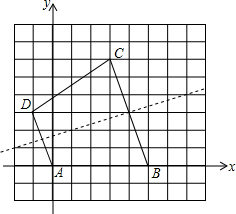
(2)如图,点P的坐标为(-2,1),(1,2),(4,3),(7,4).
四边形ABCD的面积=
| 1 |
| 2 |
(2)如图,点P的坐标为(-2,1),(1,2),(4,3),(7,4).

点评:本题考查了坐标与图形性质,角平分线上的点到角的两边距离相等的性质和等腰三角形三线合一的性质,熟记各性质是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
从1,2,3,4,5这五个数中随机取出一个数,取出的数是某个整数的平方数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
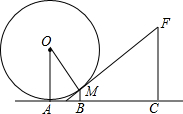 如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=
如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=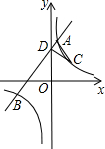 如图,已知直线y=mx+b与双曲线y=
如图,已知直线y=mx+b与双曲线y=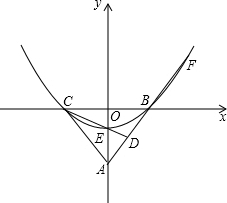 如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
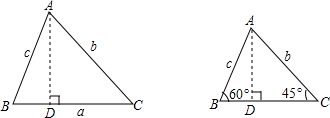 阅读下面的材料:
阅读下面的材料: 如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为
如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为